Underfrequency load shedding protection
System frequency response model with underfrequency load shedding protection
Use case purpose and context
4 simple test cases have been developed in the context of XX by University of Ljubljana.
Network description
All 4 cases are based on the Underfrequency load shedding protection scheme and SSystem frequency response model as described here
Case studies
Input data
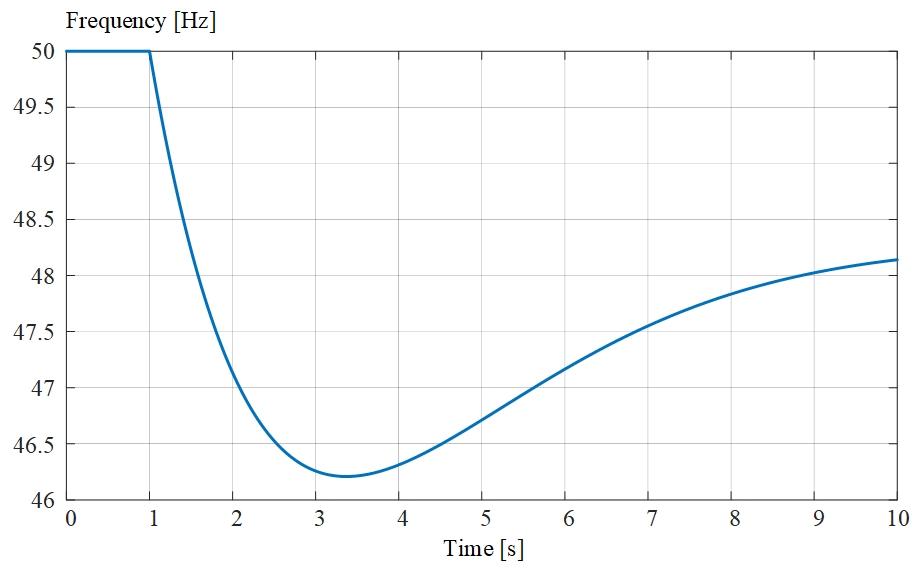
In the presented four case studies we considered a rated frequency of \(50\) \(Hz\) and the following SFRM parameters: \(H\) = \(4\), \(D\) = \(1\), \(F_H\) = \(0.3\), \(R\) = \(0.05\), \(K_M\) = \(0.95\) and \(T_R\) = \(8\).
A 10-second-long time domain simulation was carried out with a time step of \(1\) microsecond. \(\Delta P\) was modeled as a step change of \(\Delta P\) = \(-0.7\) occurring at time \(t\) = \(1\) second. A frequency limit value \(f_{LIM}\) for the calculation of \(M\) via equation (3) is \(f_{LIM}\) = \(47.5\) \(Hz\).
Case study #1: Simulation without UFLS.
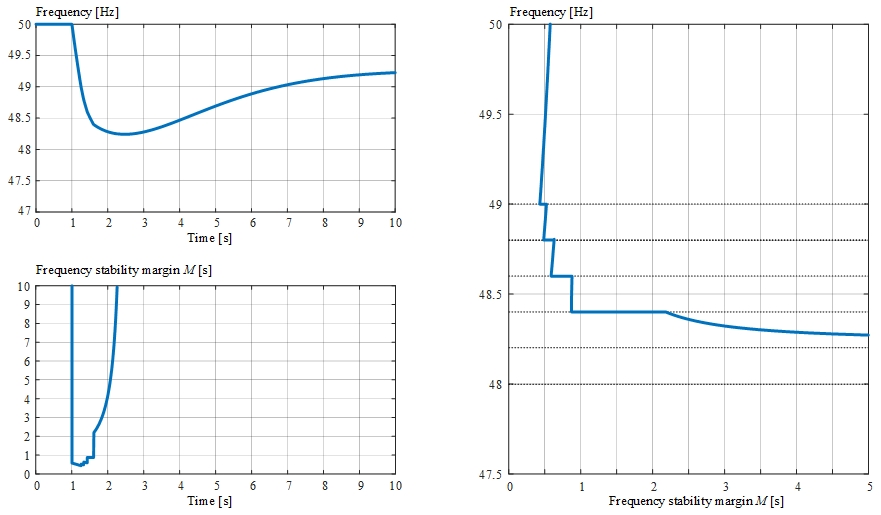
Case study #2: Simulation with conventional UFLS with the following settings:
- number of stages \(n\) = \(6\),
- stage frequency thresholds \(49.00\) \(Hz\), \(48.80\) \(Hz\), \(48.60\) \(Hz\), \(48.40\) \(Hz\), \(48.20\) \(Hz\), \(48.00\) \(Hz\),
- stage amounts \(0.10\)/stage.
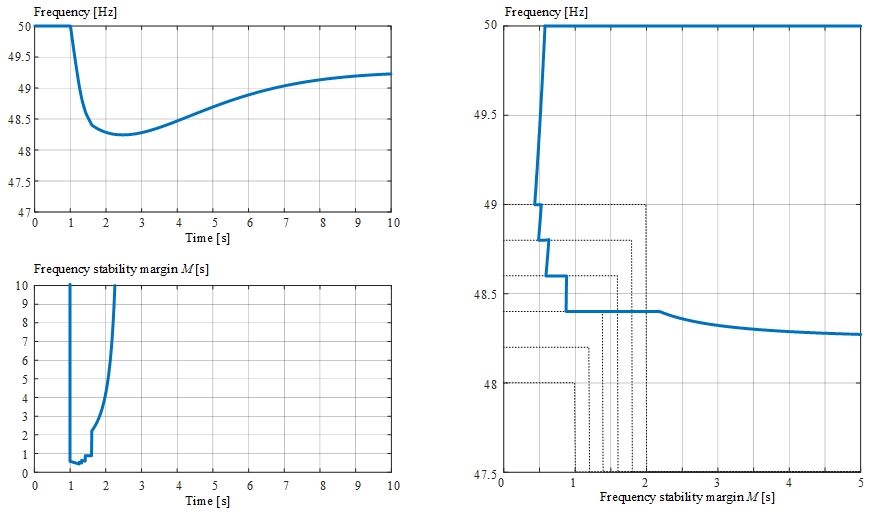
Case study #3: Simulation with innovative UFLS with the following settings:
- number of stages \(n\) = \(6\),
- stage frequency thresholds \(49.00\) \(Hz\), \(48.80\) \(Hz\), \(48.60\) \(Hz\), \(48.40\) \(Hz\), \(48.20\) \(Hz\), \(48.00\) \(Hz\),
- stage \(M\) thresholds \(2.0\), \(1.80\), \(1.60\), \(1.40\), \(1.20\), \(1.00\) seconds,
- L-shaped \(f_{thr}(M)\) threshold function
- stage amounts \(0.10\)/stage.
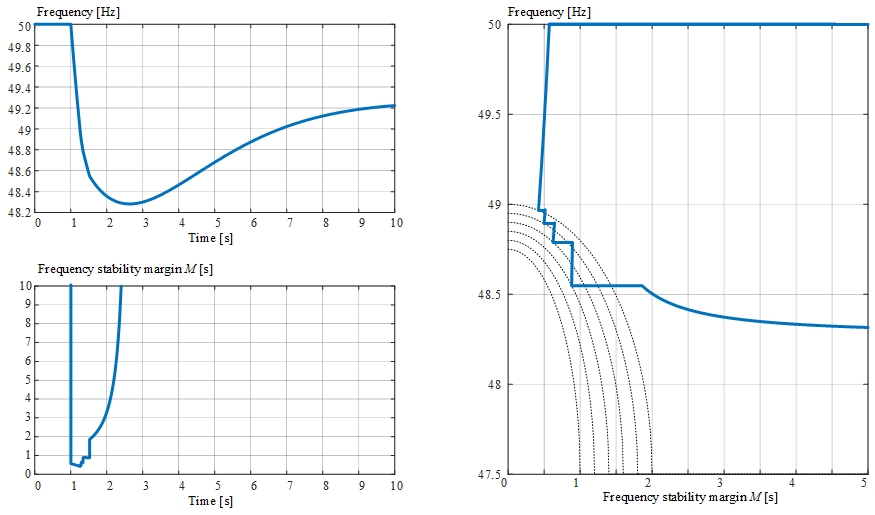
Case study #4: Simulation with innovative UFLS with the following settings:
- number of stages \(n\) = \(6\),
- stage frequency thresholds \(49.0\), \(48.95\), \(48.90\), \(48.85\), \(48.80\), \(48.75\) \(Hz\),
- stage \(M\) thresholds \(2.0\), \(1.80\), \(1.60\), \(1.40\), \(1.20\), \(1.00\) seconds,
- ellipse-shaped \(f_{thr}(M)\) threshold function
- stage amounts \(0.10\)/stage.
Case study results
The results, provided in the continuation, can be obtained by running any of the three models provided (numerical integration with Matlab, Simulink simulation, Numerical integration with Python).
Implementations
| Software | URL | Created |
|---|---|---|
| Python | Link | 03/06/2024 |
| Matlab/Simulink | Link | 03/06/2024 |
References
[1] P. M. Anderson and M. Mirheydar, ‘A low-order system frequency response model’, IEEE Trans. Power Syst., vol. 5, no. 3, pp. 720–729, Aug. 1990, doi: 10.1109/59.65898.
[2] T. Skrjanc, R. Mihalic, and U. Rudez, ‘A systematic literature review on under-frequency load shedding protection using clustering methods’, Renew. Sustain. Energy Rev., vol. 180, p. 113294, Jul. 2023, doi: 10.1016/j.rser.2023.113294.
[3] U. Rudež, ‘Method and device for improved under-frequency load shedding in electrical power systems: US 11 349 309 B2 - 2022-05-31’, 2022 [Online]. Available: https://si.espacenet.com/publicationDetails/originalDocument?FT=D&date=20220531&DB=&locale=si_SI&CC=US&NR=11349309B2&KC=B2&ND=4
[4] U. Rudez, D. Sodin, and R. Mihalic, ‘Estimating frequency stability margin for flexible under-frequency relay operation’, Electr. Power Syst. Res., vol. 194, p. 107116, May 2021, doi: 10.1016/j.epsr.2021.107116.
[5] U. Rudez and R. Mihalic, ‘RoCoF-based Improvement of Conventional Under-Frequency Load Shedding’, in 2019 IEEE Milan PowerTech, Jun. 2019, pp. 1–5. doi: 10.1109/PTC.2019.8810438.
[6] M. Vadillo, L. Sigrist, and U. Rudez, ‘Design and comparison of UFLS schemes of isolated power systems based on frequency stability margin’, in 2023 IEEE Belgrade PowerTech, Belgrade, Serbia: IEEE, Jun. 2023, pp. 1–6. doi: 10.1109/PowerTech55446.2023.10202842.
[7] U. Rudež, T. Dimitrovska, and R. Mihalič, ‘A RoCoF-based supplement to conventional under-frequency load shedding protection characteristic’, presented at the Pacworld 2019, Glasgow, Scotland: s. n.], p. Str. 1-12.
[8] D. Sodin, R. Ilievska, A. Čampa, M. Smolnikar, and U. Rudez, ‘Proving a Concept of Flexible Under-Frequency Load Shedding with Hardware-in-the-Loop Testing’, Energies, vol. 13, no. 14, Art. no. 14, Jan. 2020, doi: 10.3390/en13143607.
[9] A. Bonetti, J. Zakonjsek, and U. Rudez, ‘Bringing ROCOF into spotlight in Smart Grids: new standardization and UFLS method’, in 2020 2nd Global Power, Energy and Communication Conference (GPECOM), Oct. 2020, pp. 238–244. doi: 10.1109/GPECOM49333.2020.9248722.