GENTPF/GENTPJ Synchronous Machine with Saturation

Authors: Carlos Alegre (eRoots)

Reviewers: Eduardo Prieto Araujo (UPC), Josep Fanals Batllori (eRoots)

Context

Saturation modelling in synchronous machines is key to perform transient stability studies. Starting from the dynamic model of the Synchronous Machine, GENSAL/GENROU without saturation [1], some existing models that incorporate the saturation of the poles have been developed. There are some models that directly incorporate the saturation with some additive corrections in the dynamic equation, such as the GENROU/GENSAL with saturation, but they are somewhat obsolete [2], and mismatches between the measured field current and voltage measurements with the values predicted have been found. The GENTPF/GENTPJ models [3] described in this page are aimed to apply the saturation effects to the parameters of the machine directly using a scaling factor.

Model use, assumptions, validity domain and limitations

The model is used to perform transient stability analysis of synchronous machines, providing a more accurate representation of the physical machine. It considers that there exists saturation in the iron of the machine, and it is applied to all the inductive terms simultaneously, differently to what the GENROU/GENSAL models with additive saturation consider. Following a recommendation note from the North-America Electrical Reliability Corporation (NERC) [4], the GENTPJ is overall recommended for all the synchronous machines as it recognizes the effect of the stator current in saturation. The GENROU, GENSAL and GENTPF (the latter being exactly identical to the GENTPJ except an additive term in the saturation function) may induce significant error specially in simulations where reactive power support is considered.

The model assumptions are the following:

  • The three-phase system is balanced.
  • The air gap between the stator and rotor is non-uniform, but the relationships between the flux linkages and currents are independent of the position of the rotor when expressed in the dq0 reference frame.
  • The magnetic circuit is considered to be non-linear, considering saturation effects, and can be modeled using different saturation functions.
  • The saturation effects are applied to the subtransient reactances, but not at the transient and steady-state reactances.

The GENTPJ model is suitable for EMT as it models with detail the non-linearities and the fast dynamics of the machine. However, the saturation effects are only applied to the subtransient reactances. Newer models consider saturation in more reactances of the machine, improving GENTPF and GENTPJ models. GENTPJ will be deprecated in December 2024, and substituted by the GENQEC [5], although this later model is still in testing process [6].

Model Description

Parameters

Parameter Description Unit
\(\omega_s\) Synchronous speed rad/s
\(R_s\) Stator resistance \(\Omega\)
\(X_d\) Direct-axis synchronous reactance \(\Omega\)
\(X'_d\) Direct-axis transient reactance \(\Omega\)
\(X_q\) Quadrature-axis synchronous reactance \(\Omega\)
\(X'_q\) Quadrature-axis transient reactance \(\Omega\)
\(X''_{d}\) Direct-axis subtransient reactance \(\Omega\)
\(X''_{q}\) Quadrature-axis subtransient reactance \(\Omega\)
\(X''_{dsat}\) Direct-axis subtransient reactance with saturation considered \(\Omega\)
\(X''_{qsat}\) Quadrature-axis subtransient reactance with saturation considered \(\Omega\)
\(X_{ls}\) Stator leakage reactance \(\Omega\)
\(T'_{d0}\) Direct-axis transient time constant s
\(T''_{d0}\) Direct-axis subtransient time constant s
\(T'_{q0}\) Quadrature-axis transient time constant s
\(T''_{q0}\) Quadrature-axis subtransient time constant s
\(H\) Inertia constant s

Variables

Variable Description Unit
\(\Psi_d\) d-axis flux linkage Wb
\(\Psi_q\) q-axis flux linkage Wb
\(\Psi_0\) Zero-sequence flux linkage Wb
\(\Psi_{1d}\) Flux linkage associated with \(X''_d\) Wb
\(\Psi_{2q}\) Flux linkage associated with \(X''_q\) Wb
\(I_d\) d-axis current A
\(I_q\) q-axis current A
\(I_0\) Zero-sequence current A
\(V_d\) d-axis voltage V
\(V_q\) q-axis voltage V
\(V_0\) Zero-sequence voltage V
\(E_{fd}\) Field voltage V
\(E'_q\) Transient voltage behind transient reactance in d-axis V
\(E'_d\) Transient voltage behind transient reactance in q-axis V
\(\delta\) Rotor angle rad
\(\omega\) Electrical rotational speed rad/s
\(T_m\) Mechanical torque Nm
\(T_{fw}\) Windage and friction torque m
\(Sat_d\) Saturation factor for the d-axis Unitless

Equations

Electric Dynamics Equations:
$$ V_d = \frac{\omega}{\omega_s} E_d'' + I_q X_{qsat}'' - I_dR_a$$ $$ V_q = \frac{\omega}{\omega_s} E_q'' - I_d X_{dsat}'' - I_qR_a$$ $$ \frac{1}{\omega_s} \frac{d\Psi_0}{dt} = R_s I_0 + V_0$$ $$ E''_q = E_{q1} + E_{q2} - I_d (X_d - X''_d) $$ $$ E''_d = E_{d1} + E_{d2} + I_q (X_q - X''_q) $$ $$ E'_q = E_{q1} + E_{q2} - \frac{X'_d - X''_d}{X_d - X''_d} E_{q2} - I_d (X_d - X'_d) $$ $$ E'_d = E_{d1} + E_{d2} - \frac{X'_q - X''_q}{X_q - X''_q} E_{d2} + I_q (X_q - X'_q) $$ $$ T''_{d0} \frac{dE''_q}{dt} = -Sat_d\frac{X'_d - X''_d}{X_d - X''_d} E_{q2} $$ $$ T''_{q0} \frac{dE''_d}{dt} = -Sat_q\frac{X'_q - X''_q}{X_q - X''_q} E_{d2} $$ $$ T'_{d0} \frac{dE'_q}{dt} = E_{fd} - Sat_dE_{q1} $$ $$ T'_{q0} \frac{dE'_d}{dt} = -Sat_qE_{d1} $$
Swing equations:
$$ \frac{d\delta}{dt} = \omega - \omega_s$$ $$ \frac{2H}{\omega_s} \frac{d\omega}{dt} = T_m - (\Psi_d I_q - \Psi_q I_d) - T_{fw}$$
Electrical Torque Equations:
$$ \psi_q = \psi_q'' - I_q X''_{qsat} = -E''_d - I_q X''_{qsat} $$ $$ \psi_d = \psi_d'' - I_d X''_{dsat} = E''_q - I_d X''_{dsat} $$ $$ T_{elec} = \psi_d I_q - \psi_q I_d $$

where the following rearrangement can be done:

$$ E_{q1} = E''_q + \left( E'_q - E''_q \right) \frac{X_d - X''_d}{X_d - X'_d} = \frac{X_d - X''_d}{X_d - X'_d} E'_q - \frac{X_d - X''_d}{X_d - X'_d} E''_q $$ $$ E_{d1} = E''_d + \left( E'_d - E''_d \right) \frac{X_q - X''_q}{X_q - X'_q} = \frac{X_q - X''_q}{X_q - X'_q} E'_d - \frac{X_q - X''_q}{X_q - X'_q} E''_d $$ $$ E_{q2} = -\left( E'_q - E''_q \right) \frac{X_d - X'_d}{X_d - X''_d} + I_d (X_d - X''_d) $$ $$ E_{d2} = -\left( E'_d - E''_d \right) \frac{X_q - X'_q}{X_q - X''_q} - I_q (X_q - X''_q) $$

Operational principles

Modelling saturation

To model the saturation, there are three commonly used functions:

  • Quadratic: \(Sat(x) = B(x-A)^2\). Used in GE PSLF and PowerWorld Simulator.
  • Scaled Quadratic: \(Sat(x) = \frac{B(x-A)^2}{x}\). Used in PTI PSS/E and PowerWorld Simulator.
  • Exponential: \(Sat(x) = Bx^A\). Used in BPA-IPF nad some specific models of PTI PSS/E and PowerWorld Simualtor.

In this case, the variable will be the magnetic flux and, for the GENTPJ, the currents \(I_d\) and \(I_q\).

Diference between GENTPF and GENTPJ

The model presented has two different approaches to include the saturation, which results in two slightly different models, the GENTPF and the GENTPJ. The only difference is an additive term that models the effect of the field current. The following equations are used to calculate the saturation over the q and d axis:

$$ Sat_d = 1 + Sat(\Psi_{ag} + K_{is}\sqrt(I_d^2 + I_q^2))$$ $$ Sat_q = 1 + \frac{X_q}{X_d}Sat(\Psi_{ag} + K_{is}\sqrt(I_d^2 + I_q^2))$$

where \(K_{is}\) is a given parameter that models the stator current effect. In the GENTPF, \(K_{is} = 0\), disregarding the effect to simplify the model, while the GENTPJ, with \(K_{is} \ne 0\), is the more complete model and generally the one recommended using in transient stability studies.

This saturation factor will be used to multiply the flux values or to divide the reactance values.

Transformation of the GENSAL model

Starting form the GENSAL equations, the GENTPJ model is derived with detail in the PowerWorld document [3]. The most important aspects are covered in this section.

Subtransient reactances

When adding saturation in the GENSAL model, it is necessary to set \(X_d'' = X_q''\) to avoid transient saliency and then having a simple circuit equation could be used to model the grid connection. It was convenient to simplify the models back in the days, but it did not model properly the real behavior of the synchronous machine.

For the GENTPF/GENTPJ, generally \(X_d'' \ne X_q''\), which results in some more complex equations, but it allows to consider the impact of the transient saliency. The following expressions are used to calculate the saturated values of the reactances:

$$ X_{dsat}'' = \frac{X_d'' - X_l}{Sat_d} + X_l $$ $$ X_{qsat}'' = \frac{X_q'' - X_l}{Sat_q} + X_l $$

Network interface equations

The following circuit equations were obtained in the GENSAL model:

$$ \frac{1}{\omega_s} \frac{d\Psi_d}{dt} = R_s I_d + \frac{\omega}{\omega_s} \Psi_q + V_d$$ $$ \frac{1}{\omega_s} \frac{d\Psi_q}{dt} = R_s I_q - \frac{\omega}{\omega_s} \Psi_d + V_q$$

With proper transformations using the expressions for the fluxes, they can be rewritten as:

$$ V_d = - R_s I_d + X_q''I_q + E_d''\frac{\omega}{\omega_s}$$ $$ V_q = - R_s I_q - X_d''I_d + E_q''\frac{\omega}{\omega_s}$$

with \(E_d'' = E'_d \frac{X_q'' - X_l}{X_q' - X_l} + \Psi_q'' \frac{X_q' - X_q"}{X_q' - X_l}\), and \(E_q'' = E'_q \frac{X_d'' - X_l}{X_d' - X_l} + \Psi_d'' \frac{X_d' - X_d"}{X_d' - X_l}\), and where the scaling \(\frac{\omega}{\omega_s}\) is ommited for the subtransient reactances. As discussed for the GENSAL model, \(X_d'' = X_q''\), which allows to compact the grid interface equations in a single equation:

$$ V_d + jV_q = \frac{\omega}{\omega_s} (E_d'' + jE_q'') - (R_s + jX_d'') (I_d + jI_q) $$

This is not doable in the GENTPJ model, since generally the subtransient reactances are not equal. In this case, the saturated values of the subtransient reactance are used:

$$ V_d = \frac{\omega}{\omega_s} E_d'' + I_q X_{qsat}'' - I_dR_a$$ $$ V_q = \frac{\omega}{\omega_s} E_q'' - I_d X_{dsat}'' - I_qR_a$$

Again, the frequency factor can be added to the term \(I_q X_{qsat}''\) and \(I_d X_{dsat}''\), but it is commonly omitted in transient stability studies.

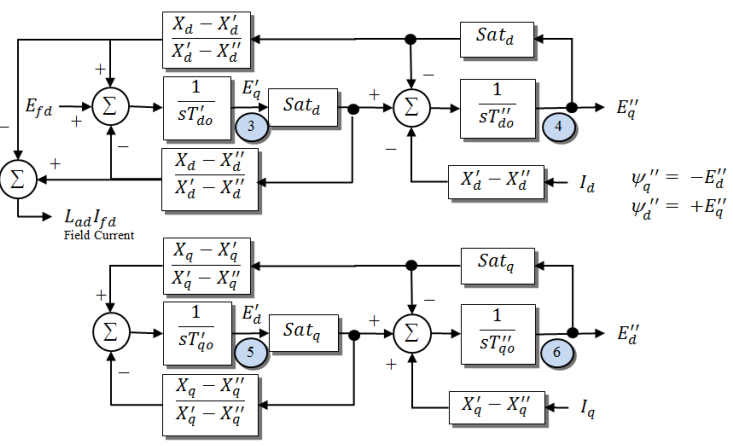
The following figure shows the block diagram for this GENTPJ model [3]:

Block diagram of the GENTPJ model

Figure 1: Block diagram of the GENTPJ model


Open source implementations

No open-source implementations were found.

Table of references

[1] Sauer, P.W.; Pai, M. A. “Power System Dynamics and Stability”, Urbana, IL, USA, 2006.

[2] P. W. Sauer, “Constraints on saturation modeling in AC machines”, in IEEE Transactions on Energy Conversion, vol. 7, no. 1, pp. 161-167, March 1992, doi: 10.1109/60.124556

[3] Weber, J. “Description of Machine Models GENROU, GENSAL, GENTPF and GENTPJ.” PowerWorld Corporation (2015). Link

[4] North American Electric Reliability Corporation (NERC). “Modeling Notification: Use of GENTPJ Generator Model” (2016). Link

[5] PowerWorld Corporation. “GENQEC Machine Model” (2022). Link

[6] Western Electricity Coordinating Council (WECC). “WECC Aproved Dynamic Model Library” (2024). Link

Evaluate